Тема 7."Основы термодинамики"
Термодинамический и молекулярно – кинетический метод исследования явлений природыВ механике не рассматривается изменение внутреннего состояния тел. Для механики, которая решает задачи о движении тела как целого, это не имеет значения. Мы говорим, что при движении часть механической энергии перешла, например, в тепловую и все. Какие процессы сопровождают переход механической энергии в тепло не уточняется. Термодинамика и молекулярно – кинетическая теория (м.к.т.) изучают внутреннее строение и состояние тел, которые могут меняться в таких процессах, как нагревание и охлаждение, тепловое расширение и сжатие, фазовые превращения, диффузия, теплопроводность и вязкость и т.д. Термодинамика и молекулярно – кинетическая теория, имея общий предмет изучения, различаются по методу исследований явлений. Термодинамика опирается на небольшое число фундаментальных законов, справедливых всегда и для всех макроскопических тел. Сведения о конкретном виде тел (например о данном газе, жидкости или твердом теле) термодинамика берет из опыта (обычно в виде так называемого уравнения состояния или зависимости физических величин от температуры или давления). При этом молекулярное строение тел остается за рамками термодинамического исследования. Молекулярно – кинетическая теория, напротив, для каждого конкретного тела создает модель его молекулярного состояния и из этой модели методами математической статистики (ввиду большого числа молекул) выводит конкретные свойства данного вещества. Методы термодинамики и м.к.т. взаимно дополняют друг друга. 9.1. Термодинамическое состояние телаТермодинамическое состояние тела (например, газа) характеризуется его массой 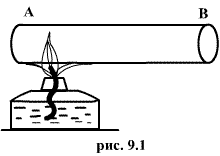 В состоянии т.д.р. для каждого вещества термодинамические параметры связаны между собой так называемым уравнением состояния:
Таким уравнением состояния для идеального газа является уравнение Менделеева – Клапейрона:
Здесь R=8,31 Дж/(мольК) – универсальная газовая постоянная, μ - молярная масса. Для углерода (С) величина μ составляет 12г, для водорода (H2) – 2г, для кислорода (О2) – 32г, для воды (Н2О) – 18г и т.д. В моле любого вещества содержится одно и то же количество молекул N0, называемое числом Авогадро:
Это объясняется тем, что значение моля любого вещества выбрано пропорциональным массе молекулы этого вещества. Масса молекулы может быть получена делением массы моля на число Авогадро:
Отношение универсальной газовой постоянной R к числу Авогадро (т.е. универсальная газовая постоянная, приходящаяся на одну молекулу) называется постоянной Больцмана:
В формулу (9.2) входят еще давление, объем, температура и масса газа. Давление Р в системе СИ измеряется в ньютонах на квадратный метр или паскалях (Н/м2=Па), объем V – в кубических метрах (м2), масса m – в килограммах (кг), температура T – в кельвинах (К). Абсолютная температура Т отсчитывается от абсолютного нуля (-273,15°С), т.е. Т=t+273,15, где t – температура по Цельсию. Если количество вещества равно 1 молю, то (9.2) превращается в
Идеальным газом называется газ, настолько разреженный, что он подчиняется уравнению (9.2) или(9.6). Смысл этого определения состоит, очевидно, в том, что для подчинения уравнению (9.6) газ должен быть достаточно разреженным. Если газ, напротив, сжат до достаточно больших плотностей (так называемый реальный газ), то вместо (9.6) имеем
Это – уравнение состояния реального газа или уравнение Ван-дер-Ваальса. Здесь a и b – постоянные. 9.2 Внутренняя энергияПод внутренней энергией (U) понимается вся энергия системы (тела) за исключением механической энергии системы как целого. Что именно входит во внутреннюю энергию системы? Сюда входит кинетическая энергия поступательного движения ее молекул, потенциальная энергия их взаимодействия между собой, энергия возбуждения колебаний и вращений молекул. Здесь перечислены лишь те виды энергии системы, которые могут меняться в рассматриваемых нами термодинамических процессах. Например, энергию возбуждения атомных ядер нужно будет включить, если будут рассматриваться температуры, при которых такое возбуждение может произойти. Поскольку состояние термодинамической системы (например, газа) определяется величинами m, μ, V, T (давление P само определяется этими же величинами), то от них должна зависеть и внутренняя энергия U. Опустим пока постоянные для данного тела m и μ (ниже примем их во внимание), запишем U=U(V,T). Зависимость внутренней энергии от объема V связана с тем, что при изменении объема меняется расстояние между молекулами и, следовательно, потенциальная энергия их взаимодействия. Эта зависимость существенна только для реального газа. Для идеального газа внутренняя энергия должна зависеть только от температуры, т.е. U=U(T), так как температура определяет среднюю кинетическую энергию молекул. 9.3 Работа газаРассмотрим газ, находящийся в цилиндре с поршнем, позволяющем менять объем газа (рис 9.2). Отметим, что слово «газ» здесь совершенно условно. Это может быть жидкость, кристалл и вообще любое тело. Цилиндр контактирует с нагревателем или холодильником, который может сообщать газу тепло или отбирать его. Пусть на поршень оказывается внешнее давление, величина которого может быть любой. 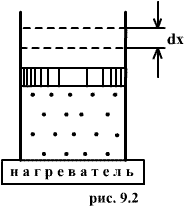 Все процессы, которые будем рассматривать ниже, будут квазистатическими, т.е. медленными настолько, чтобы можно было считать, что в каждый момент газ находится в состоянии т.д.р. Если очень быстро сжать газ, то давление его у поршня окажется на какой-то момент больше, чем в стальном объеме, и тогда нельзя будет говорить о давлении газа вообще. Такой процесс не является квазистатическим. Приближенно квазистатическими являются и процессы, достаточно быстрые с технической точки зрения, например процессы, происходящих в цилиндрах двигателя автомашины во время работы мотора (оказывается, для приближенной квазистатичности требуется, чтобы скорость поршня была мала по сравнению со скоростью звука в газе). Работа над газом выполняется внешними силами при его сжатии. Работа самого газа выполняется при его расширении. Пусть газ расширяется так, что поршень на рис.9.2 поднимается на величину dx. Тогда газ выполнит работу
Эта величина называется элементарной работой газа. Работа при расширении газа от объема V1 до V2 будет равна
Если по одной оси отложить объем газа, по другой – его давление (плоскость P – V), то работа (9.9) будет изображаться площадью под кривой P(V) (рис.9.3). Процесс расширения от объема V1 до объема V2 может происходить различным образом: например, можно при этом изолировать газ от нагревателя или, наоборот, нагревать газ и т.д. Иначе говоря, при перемещении из точки 1 в точку 2 в газе могут происходить различные процессы, даже если зафиксировано начальное и конечное состояния. В каждом процессе работа будет иметь свое значение, так как площадь под кривой процесса будет различной (кривые I, II, и III на рис.9.3). Таким образом, выполняемая газом работа зависит от процесса, который с ним происходит. Обычно (хотя это и не совсем точное выражение) говорят, что «работа газа есть функция процесса». 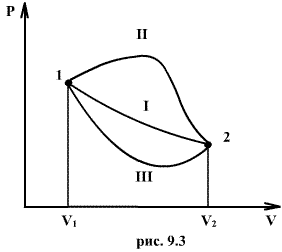 Заметим, что работа положительна, если она выполняется газом, и отрицательна, если внешние силы выполняют ее над газом. 9.4 Первый закон (начало) термодинамики.Первый закон термодинамики представляет собой закон сохранения энергии. Если сообщить телу количество тепла 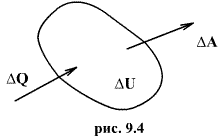 Последние выражение удобнее записать для малого изменения состояния системы, вызванного сообщением ей малого количества тепла δQ и совершением системой элементарной работы δA
Различие в записи малого приращения внутренней энергии dU и элементарного количества теплоты δQ, а также элементарной работы δA объясняется следующим соображениями. Как уже отмечалось, внутренняя энергия системы являеться функцией ее состояния. Следоватено, при любом процессе, в результате которого система вновь возвратилась в некоторое состояние, полное изменение ее внутренней энергии равно нулю. Математически это записываться в виде уравнения Таким образом: δQ = dU+δA Первый закон термодинамики формулируеться следующим образом: 9.5. Основные понятия о теплоемкости вещества.В термодинамике для характеристики тепловых свойств тел используется понятие теплоемкости. Теплоемкость - количество теплоты необходимое для нагревания тела на один Кельвин
Удельной теплоемкостью называется величина, числено равная теплоте, которую надо сообщить единице массы тела для повышения его температуры на один Кельвин:
Отсюда можно определить количество теплоты, необходимое для нагревания вещества, массы m
Молярная теплоемкость - количество тепла необходимое для нагревания одного моля вещества на один Кельвин
Воспользовавшись I законом термодинамики выражение (9.11) можно переписать в виде
откуда следует, что теплоемкость есть функция процесса, т.е. теплоемкость системы зависит от того каким образом система переходит из одного состояния в другое. Вообще говоря, таких процессов может быть сколько угодно, фактически же используются чаще всего теплоемкость при р=const(Cp) и при V=const(CV). 9.6 Изохорический процесс (V=const).Первое начало термодинамики 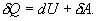 Так как при изохорическом процессе работа не совершается 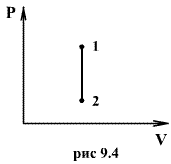 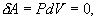 первое начало термодинамики приобретает следующий вид: 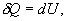 т.е. при изохорическом процессе вся подводимая к газу теплота затрачивается на увеличение внутренней энергии системы. Теплоемкость
9.7 Изобарический процесс.При изобарическом процессе элементарная работа. 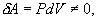 Работа системы при изменении объема от V1 до V2 определяеться следующим выражением (рис. 9.5) 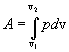 Уравнение первого начала термодинамики имеет вид 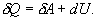 Следовательно, теплота, переданная газу при изобарическом процессе, затрачивается на увеличение его внутренней энергии и совершение работы. Из (9.16) следует, что для одного моля газа: 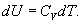 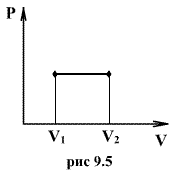 В свою очередь 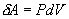 . .
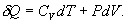 По определению изобарическая молярная теплоемкость 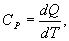 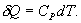 Подставляя последнее в уравнение первого начала термодинамики, получим
Определим давление Р из уравнения состояния идеального газа для одного моля газа получаем: 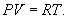 Продифференцируем по всем параметрам: 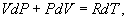 т.к. pv= const, то dP = 0 и уравнение состояния газа имеет вид: 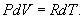 Подставим последнее в (9.17) 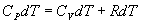
Последнее соотношение называется уравнением Майера. 9.8 Изотермический процесс.При изотермическом процессе (Т=const) dT=0 и изменение внутренней энергии dU=0. Согласно первому началу термодинамики теплота δQ, передаваемая газу, полностью затрачивается на внешнюю работу 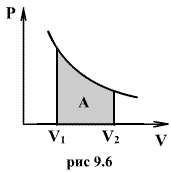 Работа системы численно равны (как известно) площади под графиком процесса в координатах P:V (рис. 9.6) Аналитическое выражение для работы следующие: 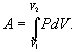 Определим из уравнения Менделеева - Клапейрона Р: 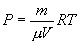 и подставим в уравнение работы
Пример. В закрытом баллоне, объем которогоРешение. Здесь имеет место процесс изотермического сжатия воздуха в баллоне. В этом случае справедливо соотношение 9.9 Адиабатический процесс.Адиабатический процесс - это такое изменение состояний газа, при котором он не отдает и не поглощает извне теплоты. Следовательно, адиабатический процесс характеризуется отсутствием теплообмена газа с окружающей средой. Адиабатическими можно считать быстро протекающие процессы. Так как передачи теплоты при адиабатическом процессе не происходит, то
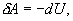 т.е. внешняя работа газа может производиться вследствие изменения его внутренней энергии. Адиабатное расширение газа (dV>0) сопровождается положительной внешней работой, но при этом внутренняя энергия уменьшается и газ охлаждается (dT<0). Сжатие газа (dV<0) соответствует отрицательной внешней работе и увеличению внутренней энергии. При этом dT>0, т.е. адиабатное сжатие газа сопровождается его нагреванием. Найдем связь между параметрами состояния идеального газа (например, Р и V) в адиабатическом процессе. Для этого перепишем (9.20) в форме 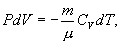 а величину 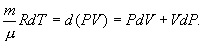 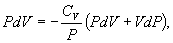 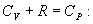 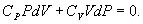 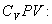 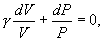 где 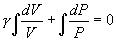 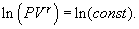
Это выражение называют уравнением Пуассона. Соотношение между давлением и температурой, а также между объемом и температурой идеального газа в адиабатическом процессе имеют вид 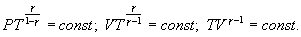 Эти соотношения легко получить из (9.21), пользуясь уравнением Менделеева - Клапейрона. Линию, изображающую адиабатический процесс в диаграмме состояния, называют адиабатой. На рис. 9.7 сплошной линией показан вид адиабаты в (P-V) диаграмме. Для сравнения в том же рисунке пунктирной линией изображена изотерма, соответствующая температуре газа в начальном состоянии 1. Так как для любого идеального газа показатель адиабаты 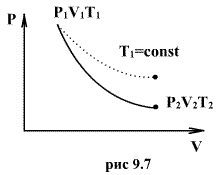 Работу, совершаемую газом в адиабатическом процессе, найдем интегрируя выражение 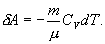 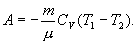 Из уравнения Майера (9.18) и выражения 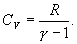
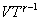 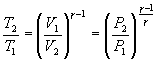 Следовательно, выражение (9.22) для работы можно представить в виде 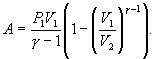 или или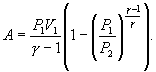 9.10. Обратимые и необратимые процессы. Круговой процесс.Обратимым процессом называют такой процесс, который может быть проведен в обратном направлении таким образом, что система будет проходить через те же состояния, что и при прямом ходе, но в обратной последовательности. Обратимым может быть только равновесный процесс. 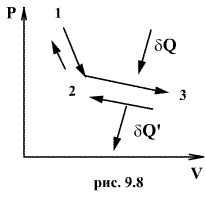 Обратимый процесс обладает следующими свойствами: если при прямом ходе на каком-то элементарном участке (рис. 9.8.) система получает тепло В том случае, когда после завершения прямого и обратного процессов система вернулась в первоначальное состояние и в окружающей среде остались изменения, процесс является необратимым. Очевидно, что все процессы в природе необратимые. 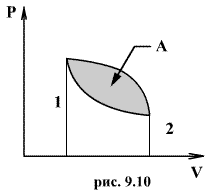 Круговым процессом (или циклом) называется такой процесс при котором система после ряда изменении возвращается в исходное состояние. На графике цикл изображается замкнутой кривой Работа совершаемая при круговом процессе, численно равна площади охватываемой кривой. После совершения цикла система возвращается в прежнее состояние. Поэтому всякая функция состояния, в частности внутренняя энергия, имеет в начале и в конце цикла одинаковое значение. 9.11 Цикл Карно.Анализируя работу тепловых двигателей, французский инженер С. Карно в 1824г. пришел к выводу, что наивыгоднейшим круговым процессом является обратимый круговой процесс, состоящий из двух изотермических и двух адиабатических процессов, т.к. он характеризуется наибольшим коэффициентом полезного действия. Такой цикл получил название цикла Карно. В прямом цикле Карно рабочее тело изотермически, а затем адиабатически расширяется, после чего снова изотермически (при более низкой температуре) и потом адиабатически сжимается. Т.е. цикл Карно ограничен двумя изотермами и двумя адиабатами. При изотермическом расширении от нагревателя отбирается тепло 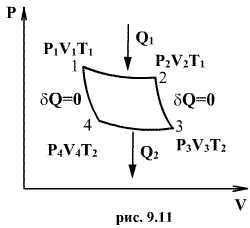 Отношение полезной работы к затраченной энергии нагревателя определяет коэффициент полезного действия (к.п.д.) тепловой машины:
Эта формула справедлива для любого обратимого и необратимого процесса. Определим коэффициент полезного действия цикла Карно для обратимого процесса. Теплота подводится на участке 1-2 и отводится на участке 3-4. Для изотермического процесса внутренняя энергия Q=const и все подводимое тепло расходуется на работу 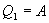 . .Тогда 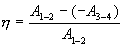 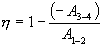 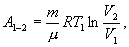 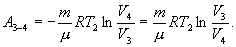
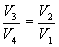 Так как процессы на участках 2-3 и 1-4 адиабатические, для определения связи между 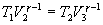 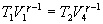 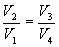 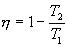 Эта формула справедлива только для обратимого цикла Карно.
9.12. Второе начало термодинамики.Выражая всеобщий закон сохранения и превращения энергии, первое начало термодинамики не позволяет определить направление протекания процесса. В самом деле, процесс самопроизвольной передачи энергии в форме теплоты от холодного тела к горячему ни в какой мере не противоречит первому закону термодинамики. Однако при опускании раскаленного куска железа в холодную воду никогда не наблюдается явление дальнейшего нагревания железа за счет соответствующего охлаждения воды. Далее, первое начало не исключает возможности такого процесса, единственным результатом которого было бы превращение теплоты, полученной от нагревателя в эквивалентную ей работу. Так, например основываясь на первом начале можно было бы попытаться построить периодически действующий двигатель, совершающий работу за счет одного источника тепла (например за счет внутренней энергии океана). Такой двигатель называется вечным двигателем второго рода. Обобщение огромного экспериментального материала привело к выводу о невозможности построения вечного двигателя второго рода. Этот вывод получил название второго начала термодинамики. Существует ряд различных по форме, одинаковых по существу формулировок второго начала:
9.13 Приведенная теплота. Равенство (неравенство) КлаузиусаРассмотрим обратимый и необратимый циклы Карно Обратимый цикл Карно.Для обратимого цикла коэффициент полезного действия можно вычислить по любой из полученных ранее формул 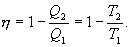 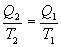 или или 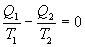
Отношение количества теплоты, подведенной к системе, к температуре, при которой это происходит, называется приведенной теплотой. Таким образом,
Так как любой замкнутый цикл можно представить как сумму бесконечного числа циклов Карно, то для любого замкнутого обратимого цикла выражение (9.26) будет справедливо и его можно записать в следующем виде
Последнее соотношение носит название равенства Клаузиуса. Необратимый цикл Карно.В этом случае 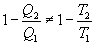 И все равенства превращаются в неравенства 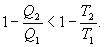 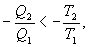 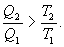 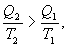 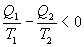 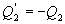 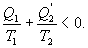 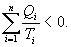
Уравнение (9.28) называется неравенством Клаузиуса. Объединяя (9.27) и (9.28), получим
Таким образом, сумма приведенных теплот любого цикла равна нулю (обратимый процесс ) или меньше нуля (необратимый процесс). 9.14 Теорема Клаузиуса.Рассмотрим обратимый процесс по пути 1а2 и 2б1. Т.к. процессе 1а2б1 обратимый, то для него справедливо равенство Клаузиуса 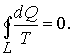 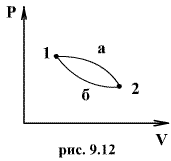 Разобьем этот интеграл на два: по пути 1а2 и 2б1 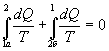 Поменяем пределы интегрирования второго интеграла 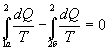 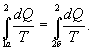 Таким образом, сумма приведенных теплот при переходе из одного состояния в другое не зависит от формы (пути) перехода в случае обратимых процессов. Последнее утверждение носит название теоремы Клаузиуса. 9.15 Энтропия.Из теоремы Клаузиуса следует, что приведенная теплота подобно энергии (потенциальной, внутренней) является функцией состояния (не зависит от пути перехода и зависит только от состояния системы). Независимость интеграла 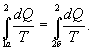 от пути перехода означает, что этот интеграл выражает собой изменение некоторой функции состояния системы, она называется энтропия и обозначается буквой S. Изменение энтропии системы, очевидно, равно
Мы говорим только об изменении энтропии (подобно изменению потенциальной энергии
9.16 Свойства энтропии.1. Обратимый процесс. В случае обратимого процесса 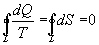 Интеграл по замкнутому контуру - это изменение энтропии во всем цикле, т.е. при обратимых циклах энтропия не меняется: 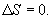 Исходя из определения энтропии можем записать, 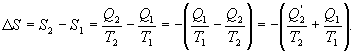 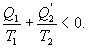 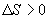
Таким образом, энтропия изолированной системы может только возрастать (если в системе протекают необратимые процессы), либо остается постоянной (если в системе протекает обратимый процесс). Убывать энтропия изолированной системы не может. 9.17 Физический смысл энтропии.Пусть имеем 2 тепловые обратимые машины с общим холодильником, но с различными нагревателями. Температура холодильника 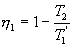 и и 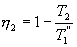 Т.к. Рассмотрим как изменяется значение энтропии рабочего тела за один цикл. Пусть температуры первой машины 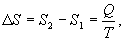 где 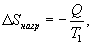 а энтропия холодильника возрастает на величину 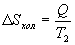 Так как Q и Изменение энтропии нагревателей (вследствие различия их температур различны 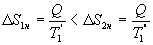 Таким, образом, изменение энтропии первой машины меньше, чем второй. 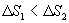 Следовательно, большему изменению энтропии рабочего тела за цикл соответствует меньший коэффициент полезного действия машины. Так как изменение энтропии холодильника одинаковое, то начальное значение энтропии больше для рабочего тела второй машины. При этом, заведомо можно сказать, что КПД второй машины меньше. Таким образом, чем больше энтропия, тем меньше коэффициент полезного действия. |
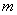 , молярной массой μ, давлением
, молярной массой μ, давлением 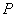 , объемом
, объемом 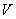 , температурой
, температурой 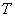 (а возможно, и другими величинами, например, определяющими его химический состав). Все эти величины называются термодинамическими параметрами тела. Однако, как будет видно из дальнейшего, такие параметры, как
(а возможно, и другими величинами, например, определяющими его химический состав). Все эти величины называются термодинамическими параметрами тела. Однако, как будет видно из дальнейшего, такие параметры, как 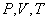 ,имеют смысл только тогда, когда тело находится, хотя бы приближенно, в так называемом состоянии термодинамического равновесия (т.д.р.). Так называется состояние, в котором все термодинамические параметры остаются со временем постоянными (к этому следует добавить еще условие отсутствия стационарных потоков). Если, например, быстро подогревать газ, как это показано на рис. 9.1, температура непосредственно подогреваемой части сосуда А окажется выше температуры части В. Не будут равны и давления в частях А и В. В этом случае не имеет смысла понятие температуры
,имеют смысл только тогда, когда тело находится, хотя бы приближенно, в так называемом состоянии термодинамического равновесия (т.д.р.). Так называется состояние, в котором все термодинамические параметры остаются со временем постоянными (к этому следует добавить еще условие отсутствия стационарных потоков). Если, например, быстро подогревать газ, как это показано на рис. 9.1, температура непосредственно подогреваемой части сосуда А окажется выше температуры части В. Не будут равны и давления в частях А и В. В этом случае не имеет смысла понятие температуры 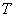 или давления
или давления 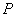 всего газа. Другой пример – впустим в газ пучок быстрых молекул. Ясно, что не имеет смысла говорить о температуре газа до тех пор, пока быстрые молекулы, вследствие ряда столкновений с другими, не приобретут скоростей порядка средней скорости остальных молекул, иначе говоря, пока система не придет в состояние т.д.р.
всего газа. Другой пример – впустим в газ пучок быстрых молекул. Ясно, что не имеет смысла говорить о температуре газа до тех пор, пока быстрые молекулы, вследствие ряда столкновений с другими, не приобретут скоростей порядка средней скорости остальных молекул, иначе говоря, пока система не придет в состояние т.д.р.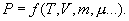
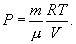
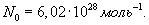
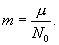
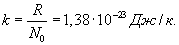
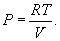
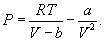
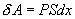 (S – площадь поршня). Получим
(S – площадь поршня). Получим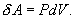
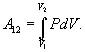
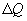 (рис.9.4), тело может за счет этого тепла увеличить свою внутреннюю энергию на величину
(рис.9.4), тело может за счет этого тепла увеличить свою внутреннюю энергию на величину 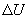 и, кроме того, выполнить работу
и, кроме того, выполнить работу 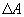 , причем в силу закона сохранения энергии: ΔQ=ΔU+ΔA
, причем в силу закона сохранения энергии: ΔQ=ΔU+ΔA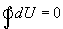 которое являеться необходимым и достаточным условием того, что внутренняя энергия системы U представляет собой, так называемый полный дифференциал dU. Работа и теплота такими свойствами не обладают. Поэтому δQ и δА не являються полными дифференциалами, эти величины являються "Функциями процесса" (см. рис. 9.3)
которое являеться необходимым и достаточным условием того, что внутренняя энергия системы U представляет собой, так называемый полный дифференциал dU. Работа и теплота такими свойствами не обладают. Поэтому δQ и δА не являються полными дифференциалами, эти величины являються "Функциями процесса" (см. рис. 9.3)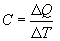
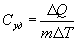
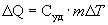
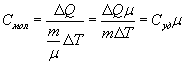
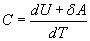
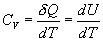
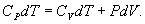
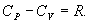
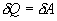 .
.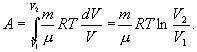
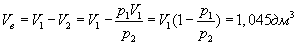
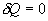 и уравнение I начала термодинамики принимает вид
и уравнение I начала термодинамики принимает вид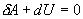
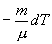 найдем из уравнения Менделеева - Клапейрона
найдем из уравнения Менделеева - Клапейрона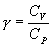 безразмерная величина, называемая постоянной адиабаты. Пренебрегая зависимостью
безразмерная величина, называемая постоянной адиабаты. Пренебрегая зависимостью 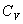 от температуры, можно считать, что для данного газа
от температуры, можно считать, что для данного газа 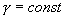 . Интегрируя последнее уравнение
. Интегрируя последнее уравнение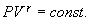
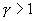 , то в (P-V) диаграмме адиабата всегда идет круче, чем изотерма. Объясняется это тем, что при адиабатическом сжатии увеличение давления обусловлено не только уменьшением объема газа, как при изотермическом сжатии, то также еще и увеличения температуры. При адиабатическом расширении температура газа уменьшается, поэтому давление газа падает быстрее, чем при изотермическом расширении.
, то в (P-V) диаграмме адиабата всегда идет круче, чем изотерма. Объясняется это тем, что при адиабатическом сжатии увеличение давления обусловлено не только уменьшением объема газа, как при изотермическом сжатии, то также еще и увеличения температуры. При адиабатическом расширении температура газа уменьшается, поэтому давление газа падает быстрее, чем при изотермическом расширении.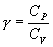 для показателя адиабаты γ следует, что
для показателя адиабаты γ следует, что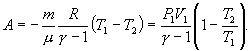
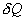 и совершает работу
и совершает работу 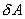 , то при обратном ходе на том же участке система отдает тепло
, то при обратном ходе на том же участке система отдает тепло 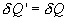 и над ней совершается работа
и над ней совершается работа 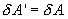 . По этой причине после протекания обратимого процесса в одном, а затем в обратном направлении и возвращение системы в первоначальное состояние в окружающих телах не должно оставаться никаких изменений. Например шарик на пружине в вакууме колеблется бесконечно долго.
. По этой причине после протекания обратимого процесса в одном, а затем в обратном направлении и возвращение системы в первоначальное состояние в окружающих телах не должно оставаться никаких изменений. Например шарик на пружине в вакууме колеблется бесконечно долго.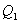 (на участке 1-2 рис. 9.11). Вследствие этого температура газа поддерживается неизменной. Соответственно, параметры точки 2 будут равны
(на участке 1-2 рис. 9.11). Вследствие этого температура газа поддерживается неизменной. Соответственно, параметры точки 2 будут равны 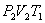 . На участке 2-3 происходит адиабатное расширение. Внутренняя энергия газа уменьшается и его температура падает до Т2. Параметры точки 3 -
. На участке 2-3 происходит адиабатное расширение. Внутренняя энергия газа уменьшается и его температура падает до Т2. Параметры точки 3 - 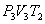 . На участке 3-4 газ изотермически сжимается. Параметры точки 4 -
. На участке 3-4 газ изотермически сжимается. Параметры точки 4 - 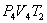 . Выделяющееся при этом тепло
. Выделяющееся при этом тепло 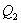 отбирается холодильником. Участок 4-1 -адиабатическое сжатие до исходного состояния, соответствующего точке 1. Таким образом, завершен цикл "1-2-3-4-1 и в итоге нагреватель отдал газу теплоту
отбирается холодильником. Участок 4-1 -адиабатическое сжатие до исходного состояния, соответствующего точке 1. Таким образом, завершен цикл "1-2-3-4-1 и в итоге нагреватель отдал газу теплоту 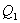 , а холодильник отобрал
, а холодильник отобрал 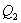 Разность
Разность 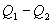 определяет полезную работу газа за один цикл, так как согласно I началу термодинамики
определяет полезную работу газа за один цикл, так как согласно I началу термодинамики 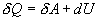 , но для кругового процесса
, но для кругового процесса 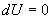 и, следовательно
и, следовательно 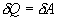 .
.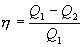
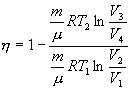
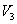 и
и 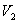 и
и 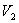 и
и 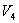 используем уравнение Пуассона в виде
используем уравнение Пуассона в виде 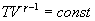
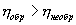
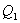 - количество тепла, подводимое к системе в процессе перехода из состояния 1 в состояние 2.
- количество тепла, подводимое к системе в процессе перехода из состояния 1 в состояние 2. 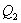 - отведенное тепло в течение изотермического процесса 3-4. Или для случая отвода тепла можно сказать, что к системе подведено
- отведенное тепло в течение изотермического процесса 3-4. Или для случая отвода тепла можно сказать, что к системе подведено 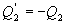 тепла. Тогда
тепла. Тогда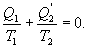
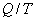 - приведенная теплота, передаваемая системе.
- приведенная теплота, передаваемая системе. 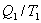 - приведенная теплота в 1 процессе.
- приведенная теплота в 1 процессе.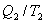 - приведенная теплота во II процессе. На участках 2-3 и 4-1 Q=0. Следовательно, это вся теплота охватывающая цикл Карно. Таким образом, для обратимого цикла Карно
- приведенная теплота во II процессе. На участках 2-3 и 4-1 Q=0. Следовательно, это вся теплота охватывающая цикл Карно. Таким образом, для обратимого цикла Карно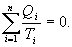
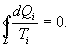
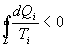
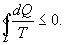
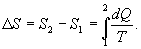
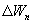 , для которой не важно где начало отсчета). Из уравнения (9.30) вытекает основное количественное выражение второго начала термодинамики
, для которой не важно где начало отсчета). Из уравнения (9.30) вытекает основное количественное выражение второго начала термодинамики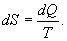
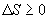
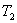 меньше температуры нагревателей
меньше температуры нагревателей 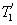 и
и 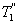 , кроме того
, кроме того 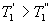 Сравним коэффициенты полезного действия машин
Сравним коэффициенты полезного действия машин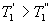 , то
, то 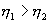 , т.е. чем больше температура нагревателя машины при общем холодильнике, тем выше КПД.
, т.е. чем больше температура нагревателя машины при общем холодильнике, тем выше КПД.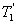 и второй
и второй 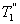 больше температуры холодильника, и пусть за каждый цикл подводится одинаковое количество теплоты. Рассмотрим для какой машины будет больше изменение энтропии
больше температуры холодильника, и пусть за каждый цикл подводится одинаковое количество теплоты. Рассмотрим для какой машины будет больше изменение энтропии 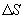
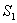 - энтропия начального состояния,
- энтропия начального состояния, 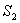 - энтропия конечного состояния; Т - температура, при которой происходит теплообмен. Энтропия нагревателя убывает на величину
- энтропия конечного состояния; Т - температура, при которой происходит теплообмен. Энтропия нагревателя убывает на величину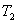 для обеих машин одинаковы, то
для обеих машин одинаковы, то 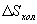 тоже одинаковы.
тоже одинаковы.