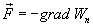Тема 4: "Энергия и работа."
4.1. Основные понятия об энергии механической системы.Мы познакомились с понятием импульса тела, являющегося мерой его поступательного движения. Однако эта динамическая характеристика тела не может служить универсальной мерой для всех форм движения. Рассмотрим равномерное прямолинейное движение тела, происходящее с трением. В этом случае сила трения 4.2. Работа.Изменение механического движения и энергии тела происходит в процессе силового взаимодействия этого тела с другими телами. Для количественной характеристики этого процесса в механике вводят понятие работы, совершаемой силой. 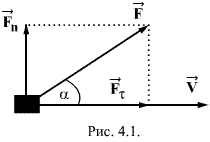 Если рассматриваемая сила
где а - угол между силой 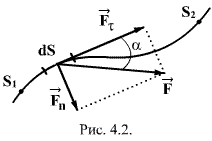 Работа - скалярная величина. Если вектор силы и вектор перемещений образуют острый угол т.е. В общем случае тело может двигаться произвольным, достаточно сложным образом (рис.4.2). Выделим элементарный участок пути
Полная работа на пути
4.3. Консервативные силы. Условие потенциальности силового поля. Силу
Изменение направления движения точки вдоль траектории на противоположное вызывает изменение знака консервативной силы, так как величина
Примером консервативных сил могут служить силы всемирного тяготения, силы упругости, силы электростатического взаимодействия заряженных тел. Поле, работа сил которого по перемещению материальной точки вдоль произвольной замкнутой траектории равна нулю, называется потенциальным. 4.4. Мощность.Величина, характеризующая скорость совершения работы, называется мощностью Мощность численно равна отношению
или в общем случае
Подставляя значение
4.5 Кинетическая энергияРассмотрим случай, когда материальная точка движется из точки 1 в точку 2 под действием приложенных к ней сил (рис.4.4.) 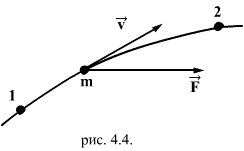 Причем силы, действующие на материальную точку, могут иметь разную природу, т.е. могут быть консервативными и неконсервативными. Уравнение движения в этом случае запишется в виде
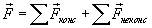 Перепишем (4.6) в виде Перепишем (4.6) в виде
Умножим скалярно уравнение (4.7) на
Учитываем то, что
называется кинетической энергией материальной точки. Таким образом, кинетическая энергия материальной точки – это энергия, которой обладает эта точка вследствие своего движения. Из полученного выражения (4.9) следует, что работа всех сил, действующих на материальную точку на участке траектории 1-2 равна изменению ее кинетической энергии на этом участке. 4.6.Потенциальная энергия.Потенциальная энергия - это энергия, обусловленная взаимным расположением тел и характером их взаимодействия. При соответствующих условиях возможно изменение потенциальной энергии, за счет чего совершается работа. Для поднятия тела массой m на высоту
знак минус перед интегралом, т.к. сила Р направлена в сторону противоположную изменению h. Проинтегрируем это выражение:
Эта энергия пойдет на увеличение энергии замкнутой системы тело-Земля т.е. численно равна
Считая поверхности Земли
Эта энергия
4.7. Закон сохранения и превращения энергии.Рассмотрим процесс изменения состояния тела, поднятого на высоту h. При этом его потенциальная энергия
Тело начало свободно падать
Кинетическая энергия тела, упавшего с высоты h, оказалась равной его потенциальной энергии, которую оно имело до начала падения. Следовательно:
На поверхности Земли h=0 и потенциальная энергия
Потенциальная энергия - уменьшается, и, следовательно, ее изменение имеет знак минус. Поэтому можем записать:
Сложив (4.12) и (4.13), получим
или Сумма
Таким образом, энергия замкнутой консервативной системы остается постоянной при всех, происходящих в ней процессах и превращениях. Энергия может переходить из одних видов в другие (механические, тепловые, и т.д.), но общее ее количество остается постоянным. Данное положение называют законом сохранения и превращения энергии. Пример. Груз массы Решение. Высота, на которую поднимется груз за первые t секунд, 4.8. Связь между потенциальной энергией и силой.Каждой точке потенциального поля соответствует, с одной стороны, некоторое значение вектора силы 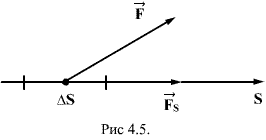 Для установления этой связи вычислим элементарную работу
где Поскольку в данном случае работа совершается за счет запаса потенциальной энергии
Из двух последних выражений получаем
Откуда
Последнее выражение дает среднее значение получить значение
Так как
Это соотношение справедливо для любого направления в пространстве, в частности и для направлений декартовых координатных осей х, у, z:
Эта формула определяет проекции вектора силы на координатные оси. Если известны эти проекции, оказывается определенным и сам вектор силы:
в математике вектор где а - скалярная функция х, у, z, называется градиентом этого скаляра обозначается символом
|
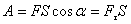
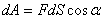
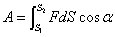
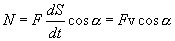
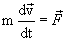
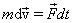
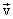 и проинтегрируем от точки1 до точки 2, получим:
и проинтегрируем от точки1 до точки 2, получим: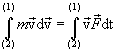
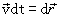 , и интеграл в правой части выражения (4.8) представляет собой работу всех сил, на участке 1-2, можно записать:
, и интеграл в правой части выражения (4.8) представляет собой работу всех сил, на участке 1-2, можно записать: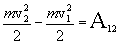
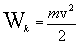
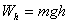
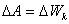
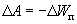
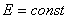
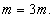
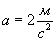 . Найти работу, произведенную в первые 1,5 с. от начала подъема.
. Найти работу, произведенную в первые 1,5 с. от начала подъема.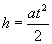 . Силу натяжения троса лебедки найдем из уравнения движения груза. На груз действуют две силы: сила тяжести mg и сила натяжения троса T. Согласно второму закону Ньютона
. Силу натяжения троса лебедки найдем из уравнения движения груза. На груз действуют две силы: сила тяжести mg и сила натяжения троса T. Согласно второму закону Ньютона  , тогда
, тогда 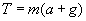 . Произведенная лебедкой работа равна
. Произведенная лебедкой работа равна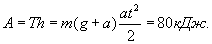
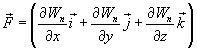
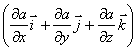 ,
,