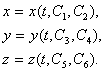Тема 3: "Динамика материальной точки и поступательного движения твердого тела"
3.1. Первый закон НьютонаПервый закон Ньютона гласит: всякое тело сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит его изменить это состояние. Первый закон Ньютона показывает, что состояние покоя или равномерного прямолинейного движения не требует для своего поддержания внешних воздействий: В этом проявляется особое динамическое свойство тел, называемое инертностью. Соответственно первый закон Ньютона обычно называют законом инерции, а движение тела, свободного от внешних воздействий - движением по инерции. 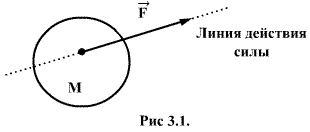 Опыт показывает, что первый закон Ньютона выполняется не во всякой системе отсчета. Системы отсчета, по отношению к которым выполняется закон инерции, называются инерциальными системами отсчета. То есть, это такие системы отсчета, относительно которых материальная точка, на которую не действуют другие тела, либо покоится, либо движется равномерно и прямолинейно. 3.2. Понятие о силе.С точки зрения наших личных наблюдений, с чем мы связываем «причину движения»? Можно ответить, с мускульной тягой или с толчком. Чтобы передвинуть стол, мы должны его очень сильно толкать, тогда как для перемещения листа бумаги по письменному столу вам достаточно лишь незначительного усилия. Эти тяговые и толкающие усилия мы называем силами. Таким образом, под силой мы понимаем физическую величину, которая является мерой механического воздействия на тело со стороны других тел. 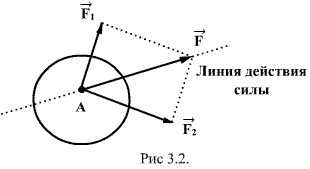 Сила, приложенная к телу, полностью определена, если указаны ее численное значение, направление действия и точка; приложения М (рис.3.1). Прямую, проведенную через точку приложения силы в направлении действия силы, называют линией действия силы. Две силы называются численно равными и противоположными по направлению, если одновременное приложение этих сил в одной и той же точке тела не вызывает изменения его механического движения. В частности, если до приложения таких двух сил тело покоилось, то оно продолжает оставаться в покое и после их приложения. Поэтому говорят, что две численно равные и противоположно направленные силы, приложенные в одной и той же точке тела, взаимно уравновешиваются. Если на тело одновременно действует n сил, приложенных в одной точке А тела, то их можно заменить одной эквивалентной силой
и приложенной в той же точке. Эта сила 3.3. Масса. Второй закон Ньютона.Опыт показывает, что под действием силы
где Величина ускорения, приобретенного под действием силы
Коэффициент пропорциональности m зависит от предмета. Его величина растет с увеличением размеров тел, если они однородны. Постоянная m называется массой тела. Масса является мерой инертности тела впоступательном движении. Чем меньше инертность тела, тем большее ускорение оно должно приобретать под действием какой-либо определенной силы. Таким образом, второй закон Ньютона можно сформулировать в следующем виде: ускорение тела прямо пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе тела. 3.4. Принцип независимости действия сил.Если на материальную точку действуют несколько сил, то
где 3.5.Третий закон НьютонаТретий закон Ньютона формулируется следующим образом: Две материальные точки действуют друг на друга с силами, которые численно равны между собой и направлены во взаимно противоположные стороны вдоль прямой, соединяющей эти точки:
Следует отметить, что силы 3.6 Преобразование координат Галилея и механический принцип относительности.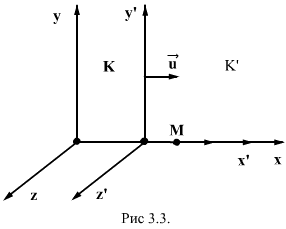  (K') Координаты тела М в системе К x:y:z , а в системе К' - x':y':z'. Эти координаты связаны между собой соотношениями, которые называються преообразованием Галилея (K') Координаты тела М в системе К x:y:z , а в системе К' - x':y':z'. Эти координаты связаны между собой соотношениями, которые называються преообразованием Галилея
Дифференцируя эти уравнения по времени и учитывая, что
Таким образом, если в системе К тело имеет ускорение а, то такое же ускорение оно имеет и в системе К'. Согласно второму закону Ньютона:
т.е. второй закон Ньютона одинаков в обоих случаях. При 3.7.Основное уравнение динамики поступательного движения материальной точки. Импульс, материальной точки.Второй закон Ньютона можно записать в другой форме. Согласно определению:
тогда
Вектор Преобразуем последнее выражение к следующему виду:
Вектор Это уравнение является выражением основного закона динамики материальной точки: изменение импульса тела равно импульсу действующей на него силы. 3.8. Центр инерции системы. В рассматриваемом выше уравнении Ньютона предполагалось, что тело имеет настолько малые размеры, что его можно считать материальной точкой. Движение любого недеформируемого тела конечных размеров может быть описано уравнениями, аналогичными (3.6), если ввести понятие «центра масс» («центра инерции») тела. Если тело состоит из n материальных точек с массами
где Соответственно соотношения между декартовыми координатами центра инерции и всех точек системы имеют вид:
Скорость центра инерции:
Импульс системы. Геометрическую сумму импульсов всех материальных точек системы называют импульсом системы и обозначают буквой
тогда скорость центра масс
Таким образом, из (3.9) следует, что импульс системы равен произведению массы всей системы на скорость ее центра инерции:
3.9. Универсальная форма второго закона Ньютона, выраженная через импульс системы.Используя выражеие для импульса
и второй закон Ньютона можем записать
где Последнее уравнение является обобщением уравнения импульса на произвольную механическую систему, т.к. ее всегда можно представить, в виде системы материальных точек, взаимодействующих друг с другом и с внешними телами. Внешними телами называются тела, не входящие в состав рассматриваемой системы, а силы, действующие на систему со стороны этих тел - внешними силами. Соответственно силы взаимодействия между материальными точками, принадлежащими рассматриваемой системе называются внутренними силами, и их равнодействующая равна нулю. Уравнение (3.11) показывает, что скорость изменения импульса механической системы равна главному вектору всех внешних сил, действующих на эту систему. 3.10. Основное уравнение динамики поступательного движения твердого тела.Используя уравнения:
можем записать
или
Таким образом, центр инерции механической системы движется как материальная точка, масса которой равна массе всей системы и на которую действует сила, равная главному вектору внешних сил, приложенных к системе. В общем случае движение твердого тела можно рассматривать как сумму двух движений: поступательного со скоростью Пример. Автомобиль двигается с места под действием постоянной силы тяги мотора Решение. Уравнение Ньютона запишется в виде:
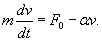
После разделения переменных, уравнение приобретает вид
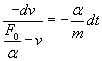
Взяв интеграл от обеих частей уравнения, получим
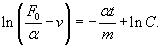
Из начальных условий () определяем константу интегрирования:
Окончательно, после потенцирования, получим 3.11.Изолированная (замкнутая) система. Закон сохранения импульса.Закон сохранения импульса является следствием второго и третьего законов Ньютона. Он имеет место в изолированной (замкнутой) системе тел. Такой системой называется механическая система, на каждое из тел которой не действуют внешние силы. В изолированной системе проявляются внутренние силы, т.е. силы взаимодействия между телами, входящими в систему. Так как в замкнутой системе внешние силы отсутствуют, то
или
Это равенство выражает закон сохранения импульса, согласно которому полный вектор импульса замкнутой системы тел с течением времени не изменяется. Т.к. Пример. Пуля вылетает из винтовки со скоростью Решение. До выстрела импульс винтовки с пулей был равен нулю. Система «винтовка-пуля» может считаться изолированной т. к. внешние силы, действующие на нее значительно меньше внутренних. Внутренние силы, это силы, возникающие при горении пороха в патроне, а внешние это сила трения и сила тяжести. Для изолированной системы, как известно, справедлив закон сохранения импульса. Тогда 3.12. Методические указания к решению задач по динамике.В классической физике, как было уже показано, состояние материальной точки полностью определяется ее координатами х, у, z. и компонентами скорости
Если считать, что результирующая сила Решая уравнение (3.14) с заданной правой частью, можно определить радиус-вектор тела в любой момент времени и, тем самым, установить вид траектории движения тела. При этом, исходя из принципа независимости движения, сложное векторное уравнение (3.14), определяющее в общем случае криволинейное движение тела, заменяют эквивалентной системой трех уравнений, каждое из которых одновременно описывает прямолинейное движение вдоль соответствующих осей х, у и z.
где
|
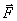 , равно их геометрической сумме
, равно их геометрической сумме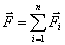
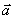 . При этом ускорение тела прямо пропорционально вызывающей его силе и совпадает с ней по направлению:
. При этом ускорение тела прямо пропорционально вызывающей его силе и совпадает с ней по направлению: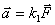
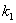 - положительный коэффициент пропорциональности, постоянный для каждого конкретного тела.
- положительный коэффициент пропорциональности, постоянный для каждого конкретного тела.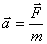
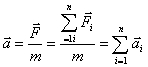
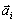 - ускорение материальной точки, вызываемое действием на нее одной силы
- ускорение материальной точки, вызываемое действием на нее одной силы 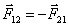
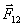 и
и 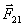 приложены к разным телам и поэтому не уравновешивают друг друга.
приложены к разным телам и поэтому не уравновешивают друг друга.
 , найдем соотношения между скоростями и ускорениями:
, найдем соотношения между скоростями и ускорениями: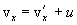
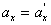
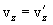
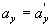
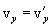
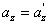
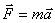
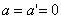 движение по инерции, т.о., справедлив и первый закон Ньютона, т.е. рассматриваемая нами подвижная система является инерциальной. Следовательно, уравнения Ньютона для материальной точки, а также для произвольной системы материальных точек одинаковы во всех инерциальных системах отсчета - инвариантны по отношению к преобразованиям Галилея. Этот результат называется механическим принципом относительности (принцип относительности Галилея), и формулируется следующим образом: равномерное и прямолинейное движение (относительно какой-либо инерциальной системы отсчета) замкнутой системы не влияет на закономерности протекания в ней механических процессов. Следовательно, в механике все инерциальные системы отсчета совершенно равноправны. Поэтому никакими механическими опытами внутри системы нельзя обнаружить движется ли система равномерно и прямолинейно или покоится.
движение по инерции, т.о., справедлив и первый закон Ньютона, т.е. рассматриваемая нами подвижная система является инерциальной. Следовательно, уравнения Ньютона для материальной точки, а также для произвольной системы материальных точек одинаковы во всех инерциальных системах отсчета - инвариантны по отношению к преобразованиям Галилея. Этот результат называется механическим принципом относительности (принцип относительности Галилея), и формулируется следующим образом: равномерное и прямолинейное движение (относительно какой-либо инерциальной системы отсчета) замкнутой системы не влияет на закономерности протекания в ней механических процессов. Следовательно, в механике все инерциальные системы отсчета совершенно равноправны. Поэтому никакими механическими опытами внутри системы нельзя обнаружить движется ли система равномерно и прямолинейно или покоится.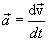 ,
,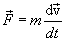 или
или 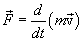
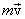 называется импульсом или количеством движения тела и совпадает по направлению с вектором скорости
называется импульсом или количеством движения тела и совпадает по направлению с вектором скорости 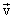 , а
, а 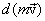 выражает изменение вектора импульса.
выражает изменение вектора импульса.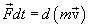
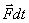 называется импульсом силы
называется импульсом силы 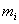 и радиус-векторами
и радиус-векторами 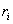 , то центром масс, системы материальных точек называют такую т.С, радиус-вектор которой определяется следующим образом:
, то центром масс, системы материальных точек называют такую т.С, радиус-вектор которой определяется следующим образом: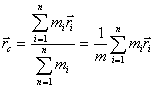
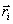 - масса и радиус-вектор i-ой точки системы, m - общая массавсей системы.
- масса и радиус-вектор i-ой точки системы, m - общая массавсей системы.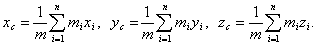
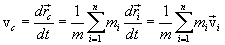
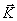 :
: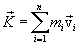 ,
,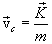
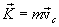
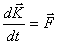
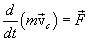
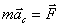
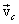 центра инерции тела, и вращения вокруг центра инерции. Поэтому последнее уравнение часто называют основным уравнением динамики поступательного движения твердого тела.
центра инерции тела, и вращения вокруг центра инерции. Поэтому последнее уравнение часто называют основным уравнением динамики поступательного движения твердого тела.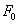 . Считая, что сила сопротивления пропорциональна скорости (
. Считая, что сила сопротивления пропорциональна скорости (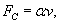 где
где 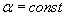 ),определить зависимость скорости автомобиля от времени.
),определить зависимость скорости автомобиля от времени.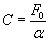 .
. 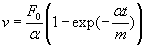 .
.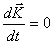
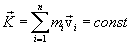
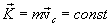 , то при любых процессах, происходящих в замкнутой системе, скорость ее центра инерции сохраняется неизменной.
, то при любых процессах, происходящих в замкнутой системе, скорость ее центра инерции сохраняется неизменной.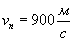 . Найти скорость винтовки при отдаче, если ее масса
. Найти скорость винтовки при отдаче, если ее масса 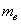
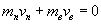 ; отсюда
; отсюда 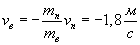 .
. в заданный момент времени, т.е. радиусом вектором частицы
в заданный момент времени, т.е. радиусом вектором частицы  и ее скоростью. С учетом указанных функциональных зависимостей второй закон Ньютона и имеет следующий вид:
и ее скоростью. С учетом указанных функциональных зависимостей второй закон Ньютона и имеет следующий вид: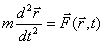
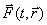 как функция координат и времени известна, то уравнение (3.14) в математической классификации представляет собой векторное дифференциальное уравнение второго порядка по отношению к радиус-вектору
как функция координат и времени известна, то уравнение (3.14) в математической классификации представляет собой векторное дифференциальное уравнение второго порядка по отношению к радиус-вектору 
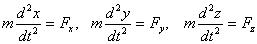
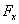 ,
, 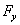 и
и 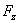 - проекции вектора
- проекции вектора 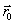 или координат
или координат 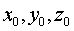 и скорости
и скорости 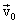 при t=0. Таким образом, в результат интегрирования уравнений (3.15) получаем координаты х, у, z как функции времени и двух констант интегрирования:
при t=0. Таким образом, в результат интегрирования уравнений (3.15) получаем координаты х, у, z как функции времени и двух констант интегрирования: