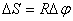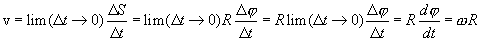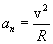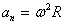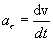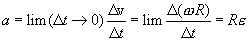Тема 2: "Кинематика вращательного движения"
|
Если в процессе движения абсолютно твердого тела (рис.2.1) его точки А и В остаются неподвижными, то и любая точка С тела, находящаяся на прямой АВ, также должна оставаться неподвижной. В противном случае расстояния АС и ВС должны были бы изменяться, что противоречило бы предположению об абсолютной твердости тела. Поэтому движение твердого тела, при котором две его точки Аи В остаются неподвижными, называют вращением тела вокруг неподвижной оси, а неподвижную прямую АВ называют осью вращения. 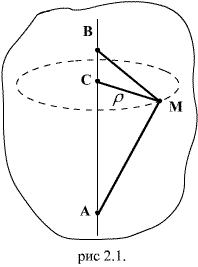 Рассмотрим произвольную точку М тела, не лежащую на оси вращения АВ. При вращении твердого тела расстояния М А и МВ и расстояние ρ точки М до оси вращения должны оставаться неизменными. Таким образом, все точки тела, вращающегося вокруг неподвижной оси, описывают окружности, центры которых лежат на оси вращения, а плоскости перпендикулярны этой оси. Движение абсолютно твердого тела, закрепленного в одной неподвижной точке, называют вращением тела вокруг неподвижной точки - центра вращения. Такое движение абсолютно твердого тела в каждый момент времени можно рассматривать как вращение вокруг некоторой оси, проходящей через центр вращения и называемой мгновенной осью вращения тела. Положение мгновенной оси относительно неподвижной системы отсчета и самого тела с течением времени может изменяться. 2.1. Угол поворота твердого тела.При вращательном движении, в отличие от поступательного, скорости Пусть т. О - центр вращения тела, а 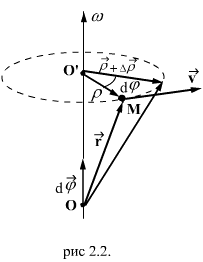 Положение произвольной т. М тела будем задавать с помощью радиус-вектора
где 2.2. Угловая скорость.Векторная величина
называется угловой скоростью тела. Вектор
т.е. при равномерном вращении 2.3.Период и частота обращения.Время, за которое тело совершает один оборот, т.е. поворачивается на угол
откуда
Число оборотов
отсюда следует, что угловая скорость
 2.4. Угловое ускорение.В случае неравномерного движения
В случае вращения тела вокруг неподвижной оси изменение вектора 2.5. Связь угловых и линейных величин.Отдельные точки вращающегося тела имеют различные линейные скорости
Линейная скорость точки по определению.
Найдем линейные ускорения точек вращающегося тела. Нормальное ускорение:
подставляя значение скорости из (2.6), находим:
Тангенциальное ускорение
 Воспользовавшись тем же отношением (2.6) получаем
Таким образом, как нормальное, так и, тангенциальное ускорения растут линейно с расстоянием точки от оси вращения. |
Пример.
Маховик начал вращаться равноускоренно и за 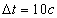 достиг частоты вращения
достиг частоты вращения 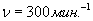 .Определить угловое ускорение
.Определить угловое ускорение 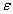 маховика и число оборотов N, которое он совершил за это время.
маховика и число оборотов N, которое он совершил за это время.
Решение.
По определению угловое ускорение 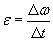 , а
, а 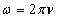 . Тогда
. Тогда 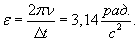
Известно, что при равноускоренном вращении, угол поворота определяется формулой 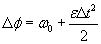 , в нашем случае
, в нашем случае 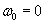 , тогда
, тогда 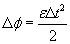 .
.
Число оборотов маховика 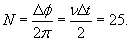
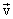 разных точек тела неодинаковы. Поэтому скорость
разных точек тела неодинаковы. Поэтому скорость 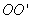 - неподвижная (или мгновенная) ось вращения (рис.2.2).
- неподвижная (или мгновенная) ось вращения (рис.2.2).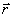 , проведенного из центра О. Из рисунка видно, что:
, проведенного из центра О. Из рисунка видно, что: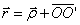 ,
,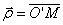 - радиус-вектор, проведенный в точку дуги окружности, по которой движется т. М. За малое время вектор
- радиус-вектор, проведенный в точку дуги окружности, по которой движется т. М. За малое время вектор 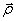 поворачивается в плоскости перпендикулярной
поворачивается в плоскости перпендикулярной 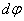 . На такой же угол поворачивается за время
. На такой же угол поворачивается за время 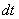 радиус-вектор любой другой точки тела, т.к в противном случае расстояние между этими точками должны были измениться. Таким образом, угол поворота характеризует перемещение всего вращающегося тела за малый промежуток времени. Удобно ввести вектор
радиус-вектор любой другой точки тела, т.к в противном случае расстояние между этими точками должны были измениться. Таким образом, угол поворота характеризует перемещение всего вращающегося тела за малый промежуток времени. Удобно ввести вектор 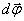 элементарного (малого) поворота тела, численно равный
элементарного (малого) поворота тела, численно равный 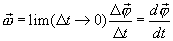
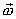 направлен вдоль мгновенной оси вращения в сторону, определяемую правилом винта, т.е. также как вектор элементарного поворота
направлен вдоль мгновенной оси вращения в сторону, определяемую правилом винта, т.е. также как вектор элементарного поворота 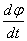 . Вращение с постоянной угловой скоростью называется равномерным, при этом:
. Вращение с постоянной угловой скоростью называется равномерным, при этом: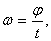
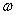 показывает, на какой угол поворачивается тело за единицу времени.
показывает, на какой угол поворачивается тело за единицу времени.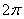 , называется периодом обращения. Так как промежутку времени
, называется периодом обращения. Так как промежутку времени 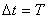 соответствует угол поворота
соответствует угол поворота 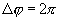 , то
, то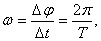
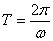
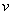 в единицу времени, очевидно, равно:
в единицу времени, очевидно, равно: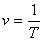
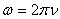
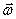 не остается постоянной. Величина, характеризующая скорость изменения угловой скорости называется угловым ускорением и равна:
не остается постоянной. Величина, характеризующая скорость изменения угловой скорости называется угловым ускорением и равна: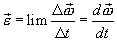
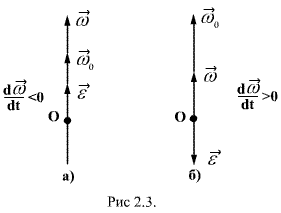
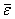 углового ускорения направлен вдоль оси вращения в ту же сторону, что и
углового ускорения направлен вдоль оси вращения в ту же сторону, что и 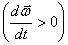 и при замедленном
и при замедленном 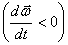 в обратном направлении. ( рис 2.3 а),б) )
в обратном направлении. ( рис 2.3 а),б) )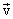 . Скорость каждой точки, будучи направлена по касательной к соответствующей окружности, непрерывно изменяет свое направление. Величина скорости
. Скорость каждой точки, будучи направлена по касательной к соответствующей окружности, непрерывно изменяет свое направление. Величина скорости 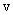 определяется скоростью вращения тела
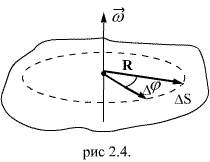
определяется скоростью вращения тела 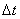 тело повернулось на угол
тело повернулось на угол 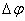 (рис 2.4). Точка, находящаяся на расстоянии R. от оси проходит при этом путь, равный
(рис 2.4). Точка, находящаяся на расстоянии R. от оси проходит при этом путь, равный