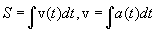Тема 1: "Кинематика поступательного движения материальной точки и твердого тела"
Тема 1: "Кинематика поступательного движения материальной точки и твердого тела"
ВведениеПредмет механики. Механикой называют раздел физики, посвященный изучению закономерностей простейшей формы движения материи - механического движения. Механика состоит из трех подразделов: кинематики, динамики и статики. Кинематика изучает движение тел без учета причин, его вызывающих. Она оперирует такими величинами как перемещение, пройденный путь, время, скорость движения и ускорение. Динамика исследует законы и причины, вызывающие движение тел, т.е. изучает движение материальных тел под действием приложенных к ним сил. К кинематическим величинам добавляются величины - сила и масса. В статике исследуют условия равновесия системы тел. Статика излагается в специальных разделах механики и здесь отдельно рассматриваться не будет. Система отсчета. Под системой отсчета понимается совокупность системы координат и часов. Понятие системы отсчета, включает в себя пространственно-временную характеристику положения тела, при этом пространственная характеристика дается с помощью координат, а временная – с помощью часов. Механическим движением называется изменение взаимного расположения тел относительно друг друга в пространстве с течением времени. Любое механическое движение относительно. Материальной точкой называется такое тело, размерами и формой которого можно пренебречь в сравнении с размерами других тел или расстояниями до них в условиях данной задачи. 1.1. Радиус-вектор материальной точки.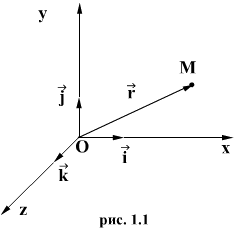 Рассмотрим движение материальной точки М в прямоугольной системе координат, поместив начало коородинат в точку О на Земле. Положение точки М относительно системы отсчета можно задать не только с помощью трех декартовых координат
Векторы 1.2.Кинематические уравнения движения материальной точки.При движении материальной точки М ее координаты Поэтому для задания закона движения м.т. необходимо указать либо вид функциональной зависимости всех трех ее координат от времени:
либо зависимость от времени радиус-вектора этой точки
Три скалярных уравнения (1.2) или эквивалентное им одно векторное уравнение (1.3) называются кинематическими уравнениями движения материальной точки. 1.3. Траектория материальной точкиТраекторией материальной точки называется линия, описываемая пространстве этой точкой при ее движении. В зависимости от формы траектории различают прямолинейное и криволинейное движения точки. Если все участки траектории точки лежат в одной плоскости, то движение точки называют плоским. Уравнения (1.2) и (1.3) задают траекторию точки в так называемой параметрической форме. Роль параметра играет время t. Решая эти уравнения совместно и исключая из них время t, найдем уравнение траектории. Длина пути. Длиной пути
1.4.Вектор перемещения.Вектором перемещения материальной 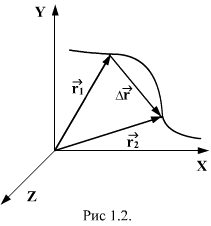 точки за время от
При прямолинейном движении вектор перемещения совпадает с соответствующим участком траектории. Из того, что перемещение является вектором, следует подтверждающийся на опыте закон независимости движений: если материальная точка участвует в нескольких движениях, то результирующее перемещение точки равно векторной сумме ее перемещений, совершаемых ею за тоже время в каждом из движений порознь. 1.5. Скорость.Для характеристики движения материальной точки вводят векторную физическую величину - скорость, определяющую как быстроту движения, так и направление движения в данный момент времени. 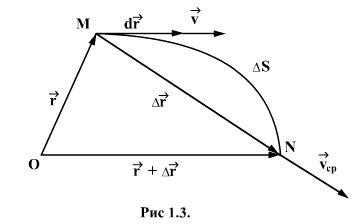 Пусть материальная точка движется по криволинейной траектории МN так, что в момент времени t она находится в т.М, а в момент времени Вектором средней скорости
Вектор средней скорости направлен также, как вектор перемещения Пример. Скорость поезда между двумя пунктами Решение. Обозначим время в пути буквой t. Из условия задачи следует, что Решая эту систему, найдем
Мгновенная скорость или скорость в данный момент времени. Если в выражении (1.5) перейти к пределу, устремляя
В процессе уменьшения величины
где Подставляя в (1.6) значения для радиус-вектора материальной точки (1.1) и выполнив почленное дифференцирование, получим:
Из сопоставления выражений (1.7) и (1.8) следует, что проекции скорости материальной точки на оси прямоугольной декартовой системы координат равны первым производным по времени от соответствующих координат точки:
Поэтому численное значение скорости:
Движение, при котором направление скорости материальной точки не изменяется, называется прямолинейным. Если численное значение мгновенной скорости точки остается во время движения неизменным, то такое движение называется равномерным. Если же за произвольные равные промежутки времени точка проходит пути разной длины, то численное значение ее мгновенной скорости с течением времени изменяется. Такое движение называют неравномерным. В этом случае часто пользуются скалярной величиной
Т.к.
Закон сложения скоростей. Если материальная точка одновременно участвует в нескольких движениях, то результирующее перемещения
В соответствии с определением (1.6):
Таким образом, скорость 1.6. Ускорение.Ускорение характеризует быстроту изменения скорости, т.е. изменение величины скорости за единицу времени. Вектор среднего ускорения. Отношение приращения скорости
Вектор, среднего ускорения совпадает по направлению с вектором Ускорение, или мгновенное ускорение равно пределу среднего ускорения при стремлении промежутка времени
В проекциях на соответствующие координаты оси:
или
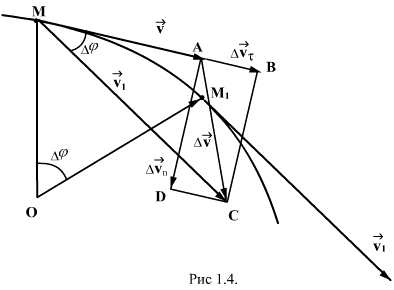 1.7. Криволинейное движение. Тангенциальное и нормальное ускорения.При прямолинейном движении векторы скорости и ускорения совпадают с направлением траектории. Рассмотрим движение материальной точки по криволинейной плоской траектории. Вектор скорости в любой точке траектории направлен по касательной к ней. Допустим, что в т.М траектории скорость была
Для этого перенесем
По определению:
Тангенциальное ускорение
Нормальное ускорение
Для этого проведем перпендикуляр через точки М и М1 к касательным к траектории (рис. 1.4) Точку пересечения обозначим через О. При достаточно малом
или
Но
Переходя к пределу при
Так как при Полное ускорение определяется векторной суммой тангенциального нормального ускорений (1.15). Так как векторы этих ускорений взаимноперпендикулярны, то модуль полного ускорения равен:
Направление полного ускорения определяется углом между векторам
1.8. Методические указания к решению задач по кинематике.Анализируя полученные формулы, в кинематике можно выделить четыре основных типа задач: 1. Общая прямая задача кинематики: по известной зависимости радиуса-вектора от времени 2. Общая обратная задача кинематики: по известным векторам скорости 3. Частная прямая задача кинематики: по известной зависимости пути от времени
Векторы 4. Частная обратная задача кинематики: по известным зависимостям скорости
|
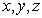 , но также с помощью одной векторной величины
, но также с помощью одной векторной величины 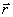 - радиуса-вектора точки М, проведенного в эту точку из начала системы координат (рис. 1.1). Если
- радиуса-вектора точки М, проведенного в эту точку из начала системы координат (рис. 1.1). Если 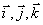 - единичные вектора (орты) осей прямоугольной декартовой системы координат, то
- единичные вектора (орты) осей прямоугольной декартовой системы координат, то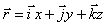
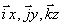 представляют собой составляющие компоненты радиуса-вектора
представляют собой составляющие компоненты радиуса-вектора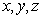 .
.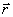 изменяются с течением времени t.
изменяются с течением времени t.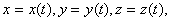
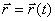
 материальной точки называют сумму длин всех участков траектории, пройденных точкой за рассматриваемый промежуток времени.
материальной точки называют сумму длин всех участков траектории, пройденных точкой за рассматриваемый промежуток времени.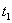 до
до 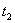 называют вектор, проведенный из положения этой точки в момент
называют вектор, проведенный из положения этой точки в момент 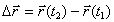
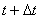 в т. N. Радиус-векторы точек М и N соответственно равны
в т. N. Радиус-векторы точек М и N соответственно равны 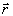 и
и 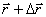 , а длина дуги МN равна
, а длина дуги МN равна 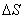 (рис. 1.3).
(рис. 1.3).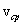 точки в интервале времени от t до t+Δt называют отношение приращения
точки в интервале времени от t до t+Δt называют отношение приращения 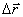 радиуса-вектора точки за этот промежуток времени к его величине
радиуса-вектора точки за этот промежуток времени к его величине 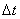 :
: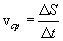
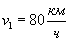 , средняя скорость на всем пути
, средняя скорость на всем пути 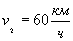 , причем остановки занимают время
, причем остановки занимают время 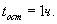
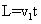
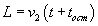 .
.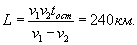
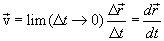
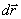 и скорость v движущейся точки направлены по касательной траектории в сторону движения. Вектор скорости v материальной точки можоразложить на три составляющие, направленные вдоль осей прямоугольной декартовой системы координат.
и скорость v движущейся точки направлены по касательной траектории в сторону движения. Вектор скорости v материальной точки можоразложить на три составляющие, направленные вдоль осей прямоугольной декартовой системы координат.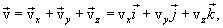
 - проекции вектора скорости на оси координат х, у, z.
- проекции вектора скорости на оси координат х, у, z.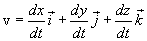
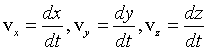
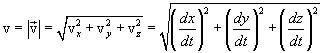
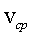 , называемой средней путевой скоростью неравномерного движения на данном участке
, называемой средней путевой скоростью неравномерного движения на данном участке 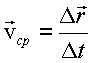
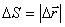 только в случае прямолинейного движения с неизменной по направлению скоростью, то в общем случае:
только в случае прямолинейного движения с неизменной по направлению скоростью, то в общем случае: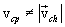 .
.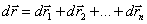
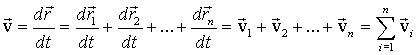
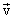 результирующего движения равна геометрической сумме скоростей
результирующего движения равна геометрической сумме скоростей 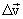 к промежутку времени
к промежутку времени 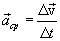
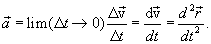
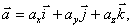
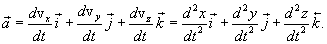
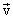 , а в т.М1 стала
, а в т.М1 стала 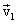 . При этом считаем, что промежуток времени при переходе точки на пути
. При этом считаем, что промежуток времени при переходе точки на пути 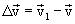
 МАС, построенного на векторах скоростей, как на сторонах. Разложим вектор
МАС, построенного на векторах скоростей, как на сторонах. Разложим вектор 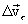 и
и 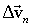 . Таким образом вектор изменения скорости
. Таким образом вектор изменения скорости 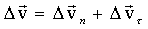
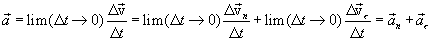
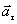 характеризует быстроту изменения скорости движения по численному значению и направлена по касательной к траектории.
характеризует быстроту изменения скорости движения по численному значению и направлена по касательной к траектории.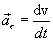
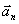 характеризует быстроту изменения скорости по направлению. Вычислим вектор:
характеризует быстроту изменения скорости по направлению. Вычислим вектор: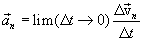
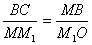
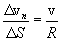
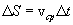 , тогда:
, тогда: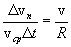
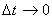 и учитывая, что при этом
и учитывая, что при этом 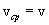 , находим:
, находим: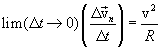 ,
,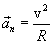
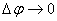 , направление этого ускорения совпадает с направлением нормали к скорости
, направление этого ускорения совпадает с направлением нормали к скорости 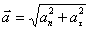
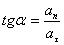
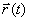 необходимо определить, векторы скорости
необходимо определить, векторы скорости 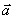 и их модули v и а, нормальную
и их модули v и а, нормальную 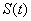 необходимо найти скорость
необходимо найти скорость 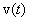 и ускорение
и ускорение 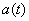 тела. В этом случае можно определить лишь модуль скорости и ускорения:
тела. В этом случае можно определить лишь модуль скорости и ускорения: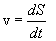 и
и 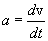 .
.